División de un segmento a una razón dada

Analiza los siguientes videos y anota las fórmulas que en ellos se muestran.

Leer mas...

Distancia entre dos puntos

Cuando los puntos se encuentran ubicados sobre el eje x o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus abscisas.
Ejemplo: La distancia entre los puntos (-4,0) y (5,0) es 4 + 5 = 9 unidades.
Cuando los puntos se encuentran ubicados sobre el eje y o en una recta paralela a este eje, la distancia entre los puntos corresponde al valor absoluto de la diferencia de sus ordenadas.
Ahora si los puntos se encuentran en cualquier lugar del sistema de coordenadas, la distancia queda determinada por la relación:

Para demostrar esta relación se deben ubicar los puntos A(x₁,y₁) y B(x₂,y₂) en el sistema de coordenadas, luego formar un triángulo rectángulo de hipotenusa AB y emplear el teorema de pitágoras.

Ejemplo: Calcula la distancia entre los puntos A(7,5) y B (4,1)

d = 5 unidades

Leer mas...

Regiones en el Plano Cartesiano

Leer mas...

lugar Geométrico

Un lugar geométrico es un conjunto de puntos que satisfacen determinadas propiedades geométricas.

Los lugares geométricos que estudiaremos serán los siguientes:

• Una recta es el conjunto de todos los puntos del plano, donde las coordenadas de cada punto obedecen una relación de primer grado
• La circunferencia es el lugar geométrico de los puntos cuya distancia a un punto determinado, el centro, es un valor dado (el radio).
• La elipse es el lugar geométrico de los puntos tales que la suma de su distancia a dos puntos fijos, los focos, es una constante dada (equivalente a la longitud del semieje mayor de la elipse).
• La parábola es el lugar geométrico de los puntos cuya distancia a un foco equivale a su distancia a una recta llamada directriz.

Leer mas...

Introducción a la Geometría Analítica

Se conoce como geometría analítica al estudio de ciertas líneas y figuras geométricas aplicando técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas.

Lo novedoso de la geometría analítica es que permite representar figuras geométricas mediante fórmulas del tipo f(x, y) = 0, donde f representa una función u otro tipo de expresión matemática.

La idea que llevó a la geometría analítica fue: a cada punto en un plano le corresponde un par ordenado de números y a cada par ordenado de números le corresponde un punto en un plano.Lo novedoso de la geometría analítica es que permite representar figuras geométricas mediante fórmulas del tipo f(x, y) = 0, donde f representa una función u otro tipo de expresión matemática.

Fue inventada por René Descartes y por Pierre Fermat, a principios del siglo XVII, y como vimos, relaciona la matemática y el álgebra con la geometría por medio de las correspondencias anteriores.

Además, Descartes y Fermat observaron, y esto es crucial, que las ecuaciones algebraicas corresponden con figuras geométricas. Eso significa que las líneas y ciertas figuras geométricas se pueden expresar como ecuaciones y, a su vez, las ecuaciones pueden graficarse como líneas o figuras geométricas.

En particular, las rectas pueden expresarse como ecuaciones polinómicas de primer grado y las circunferencias y el resto de cónicas como ecuaciones polinómicas de segundo grado.

Por lo expresado anteriormente, podemos aventurar una definición más sencilla para la geometría analítica: Rama de la geometría en que las líneas rectas, las curvas y las figuras geométricas se representan mediante expresiones algebraicas y numéricas usando un conjunto de ejes y coordenadas.

En la práctica, eso significa que cualquier punto del plano se puede localizar con respecto a un par de ejes perpendiculares (Plano cartesiano) anotando las distancias desde dicho punto a cada uno de los ejes.

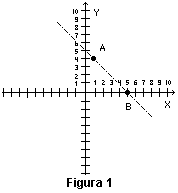
Por ejemplo, en la figura 1, el punto A está a 1 unidad hacia la derecha en el eje horizontal (x) y a 4 unidades hacia arriba en el eje vertical (y). Las coordenadas del punto A son, por tanto, 1 y 4, y el punto queda fijado con las expresiones x = 1, y = 4.Los valores positivos de x están situados a la derecha del eje y, y los negativos a la izquierda; los valores positivos de y están por encima del eje x y los negativos por debajo. Así, el punto Bde la figura 1 tiene por coordenadas x = 5, y = 0. En general, una línea recta se puede representar siempre utilizando una ecuación lineal con dos variables, x e y, de la forma ax + by + c = 0. De la misma manera, se pueden encontrar fórmulas para la circunferencia, la elipse y otras cónicas y curvas regulares.

Ahora tenemos claro que la geometría analítica se desenvuelve en el llamado Plano cartesiano, y si recordamos, como ya dijimos, que Descartes y Fermat observaron la correspondencia entre las ecuaciones algebraicas y las figuras geométricas, podemos colegir que los dos objetivos (o problemas) fundamentales de la geometría analítica son:

1.- Dada la descripción geométrica de un conjunto de puntos o lugar geométrico (una línea o una figura geométrica) en un sistema de coordenadas, obtener la ecuación algebraica que cumplen dichos puntos.

Para este objetivo, siguiendo con el ejemplo anterior, todos los puntos que pertenecen a la línea recta que pasa por A y B cumplen la ecuación lineal x + y = 5; lo que expresado de modo general es  ax + by = c.

2.- El segundo objetivo (o tipo de problema) es: dada una expresión algebraica, describir en términos geométricos el lugar geométrico de los puntos que cumplen dicha expresión.

Invirtiendo el ejemplo anterior, dada la ecuación algebraica x + y = 5, podemos calcular todos los valores para x e y que la cumplan y anotados esos valores en el Plano cartesiano veremos que corresponden a la recta AB.

Usando ecuaciones como éstas, es posible resolver algebraicamente esos problemas geométricos de construcción, como la bisección de un ángulo o de una recta dados, encontrar la perpendicular a una recta que pasa por cierto punto, o dibujar una circunferencia que pasa por tres puntos dados que no estén en línea recta.

La geometría analítica ha tenido gran importancia en el desarrollo de las matemáticas pues ha unificado los conceptos de análisis (relaciones numéricas) y geometría (relaciones espaciales).

Leer mas...